近日，信息科學與工程學院徐敬可副教授作為第一作者在《IEEE Transactions on Information Theory》在線發表了題為“Explicit Constructions of Capacity-Achieving T-PIR Schemes over Small Fields via Generalized Minor Matrices”的研究論文。該工作是徐敬可老師自2024年以來在該CCF-A期刊（IEEE TIT）上發表的又一重要進展。

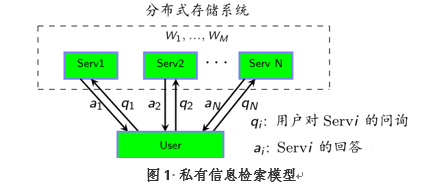
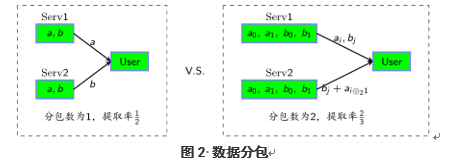
私有信息檢索（Private Information Retrieval, PIR），是信息安全領域的一個重要研究課題，主要關注的是如何在不泄露查詢內容的前提下，從多個數據庫中提取檢索信息，如1圖所示。PIR自從提出以來，已在軍事、商業等領域有著重要應用。容量是衡量PIR方案效率的重要指標，而數據分包是設計達到容量的PIR方案的重要技術，如圖2所示。然而現有的最優方案需要在很大的域上構造，這嚴重制約了方案的實用性。

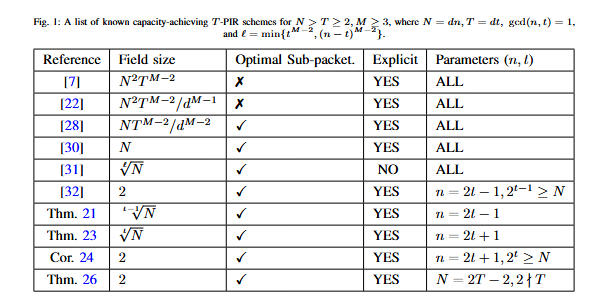
為了克服這一困難，本文創造性提出基于小域上MDS陣列碼來構造的最優PIR方案。具體來說，首先利用M-1個具有特定類型信息集的MDS陣列碼，設計了小域上分包最優且達到容量抗合謀保密信息提取方案的一般框架，從而最優PIR方案的構造問題轉化為小域上具有特定信息集的MDS陣列碼的構造問題。其次，利用乘積碼與組合技巧將該問題轉化為構造一個具有特定信息集的MDS陣列碼。然后，應用加群陪集、Trace函數、冪和、線性化多項式的牛頓恒等式等理論基礎發展出廣義子式矩陣這一工具，進而刻畫其各階順序主子式。最終，我們基于廣義子式矩陣這一最新理論工具，成功構造出三大類小域上的最優PIR方案，具有結果與比較如表1所示。

本文的合作者還有山東大學方偉軍教授。該研究得到了國家重點研發計劃項目、國家自然科學基金項目、山東省自然科學基金項目、山東省泰山學者項目、山東省“青創團隊計劃”項目的資助。

原文鏈接：https://ieeexplore.ieee.org/document/10980207.

編      輯：萬    千 

審      核：賈    波